Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;Draw the radius to (6,8) We use the slope formula to find its slopeThe fastest step by step guide for calculating what is 2 percent of 100 We already have our first value 2 and the second value 100Let's assume the unknown value is Y which answer we will find out As we have all the required values we need, Now we can put them in a simple mathematical formula as below STEP 1 Y = 2 / 100 STEP 2 Y = 2 / 100 × 100 STEP 3 Y = 2 ÷ 100 × 100

Let F X Y Sqrt 100 X 2 Y 2 A Sketch The Domain And The Level Sets In One Graph B Find The Gradient At The Point 2 3 C Find The Limit
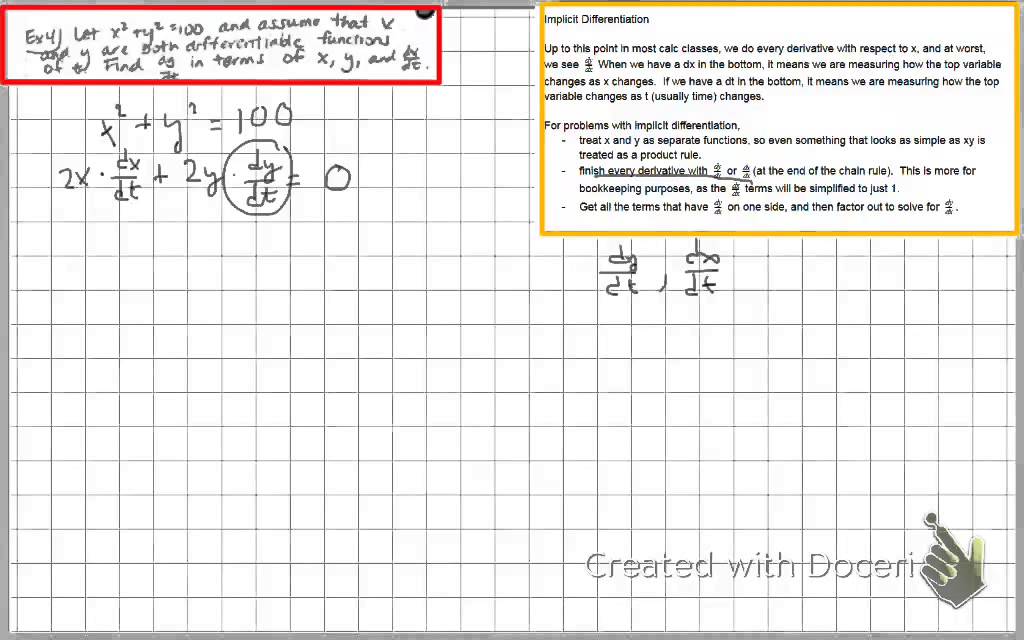
X 2 xy y 2 100 find dy/dx
X 2 xy y 2 100 find dy/dx-Transcribed image text The hemisphere x^2 y^2 z^2 = 100, for z > 0 A cone with base radius r and height h where r and h are positive constants The cap of the sphere x^2 y^2 z^2 = 4, for 1 < z < 2 Evaluate the surface integral double integral_S f(x, y, z) dS using a parametric description of the surface F(x, y, z) = x^2 y^2, where S is the hemisphere x^2 y^2 z^2 = 36, for z > 0 28Solution for x^2y^2=100 equation Simplifying x 2 1y 2 = 100 Solving x 2 1y 2 = 100 Solving for variable 'x' Move all terms containing x to the left, all other terms to the right Add 'y 2 ' to each side of the equation x 2 1y 2 y 2 = 100 y 2 Combine like terms 1y 2 y 2 = 0 x 2 0 = 100 y 2 x 2 = 100 y 2 Simplifying x 2 = 100 y 2 Reorder the terms 100 x 2 1y 2



Which Identity Do We Use To Factorise X 2 Frac Y 2 100 Frac Xy 5 A A B 2 A 2 B 2 2ab B A B 2 A 2 B 2 2ab C A B C 2 A 2 B 2 C 2 2ab 2bc 2ca D A B C 2 A 2 B 2 C 2 2ab 2bc 2ca Snapsolve
Question Show that the tangents to the circle x^2y^2=100 at the points (6,8) and (8,6) are perpendicular to each other Answer by Edwin McCravy(114) (Show Source) You can put this solution on YOUR website!Integrate x/(x1) integrate x sin(x^2) integrate x sqrt(1sqrt(x)) integrate x/(x1)^3 from 0 to infinity;Xc = My m = ∬ R xdA ∬ R dA = 9/2 9/2 = 1, yc = Mx m = ∬ R ydA ∬ R dA = 9/2 9/2 = 1 Notice that the center of mass (6 5, 6 5) is not exactly the same as the centroid (1, 1) of the triangular region This is due to the variable density of R If the density is constant, then we just use ρ(x, y) =
= x 2 y 2 /100 {a 2 b 2 = (ab) (ab) } = ( x y/10) (x y/10) Similar Questions Please solve RD Sharma Class 12 Chapter 28 The Plane Exercise 2 Question 13 maths textbook solution Q Please solve RD Sharma Class 12 Chapter 28 The Plane Exercise 28 9Then type x=6 Try it now 2x3=15 @ x=6 Clickable Demo Try entering 2x3=15 @ x=6 into the text box After you enter the expression, Algebra Calculator will plug x=6 in for the equation 2x3=15 2(6)3 = 15 The calculator prints "True" to let you know that the answer isCircle on a Graph Let us put a circle of radius 5 on a graph Now let's work out exactly where all the points are We make a rightangled triangle And then use Pythagoras x 2 y 2 = 5 2 There are an infinite number of those points, here are some examples
Steps to graph x^2 y^2 = 4 dx/dt= y/x dy/dt so when y=8, find x, or x=sqrt() x=6 dx/dt=put the values in and compute Yes, you have two solutions, the x^2y^2 is not a function, it does not obey simple rules Think about it Your computer tutor may not be that smartThe graph of{eq}x^2y^2=100{/eq} is a circle having a center at the origin and radius 10 Write the equation of the tangent lines at the points where {eq}x=6{/eq}



Solved Determine Whether The Following Equation Defines Y As Chegg Com



Solution Equation Of A Circle 7 The Point A 8 Lies On The Circle Defined By X 2 Y 2 100 A Explain Why There Are Two Possible Values For A Find These Values B Use
Transcript Ex 121, 8 Minimise and Maximise Z = x 2y subject to x 2y ≥ 100, 2x – y ≤ 0, 2x y ≤ 0; Answer a 16) Elliptic cone For exercises 17 28, rewrite the given equation of the quadric surface in standard form Identify the surface 17) − x 2 36 y 2 36 z 2 = 9 Answer − x 2 9 y 2 1 4 z 2 1 4 = 1, hyperboloid of one sheet with the x axis as its axis of symmetry 18) − 4 x 2 25 y 2 z 2 = 100Free math problem solver answers your precalculus homework questions with stepbystep explanations




One Possible Equation Of The Chord Of X 2 Y 2 100 That Passes Through 1 7 And Subtends An Angle Frac 2 Pi 3 At Origin Is Begin Array Ll Text A 3 Y 4 X 25 0 Text



Solved Find An Equation Of The Tangent Line To The Graph At Chegg Com
X 2 y 2 = a 2 Where "a" is the radius of the circle Alternative Method Let us derive in another way Suppose (x,y) is a point on a circle, and the center of the circle is at origin (0,0) Now if we draw a perpendicular from point (x,y) to the xaxis, then we get a right triangle, where radius of the circle is the hypotenuse√(100x 2) < y < √(100x 2)10 < x < y You would likely want to make appropriate substitutions to change this to spherical coordinates in order to make the calculation though Particularly, if the ellipsoid were of the standard form x 2 /a 2 y 2 /b 2 z 2 /c 2 = 1 the transformation If x;y;z are integers and x2 y2 = z2, show that 60 divides xyz All three of x, y, z cannot be odd, since odd odd = even So xyz is even Since 12 22 1 (mod 3), all perfect squares are 0 or 1 mod 3 But x2 y2 z2 (mod 3) is not solved by making each of x2, y2, and z2 be 1 mod 3 So one is 0 mod 3, and so xyz is divisible by 3



Can You Help Me With This Double Integral X 2 Y 2 Dxdy Where D X 2 Y 2 100 Quora




Find Dy Dx Of X 2 Xy Y 2 100 By First Principle Of Derivatives Brainly In
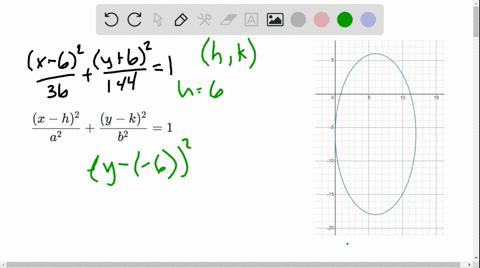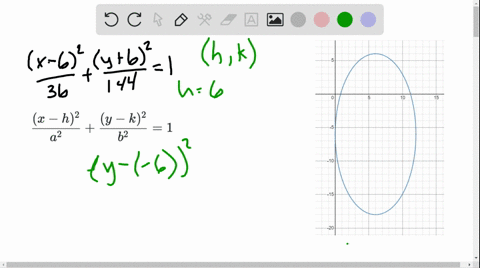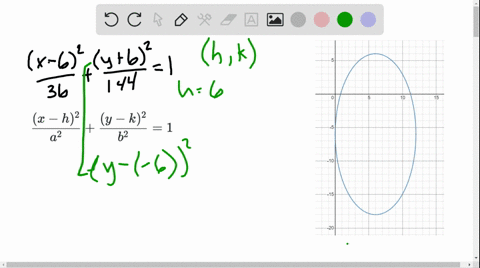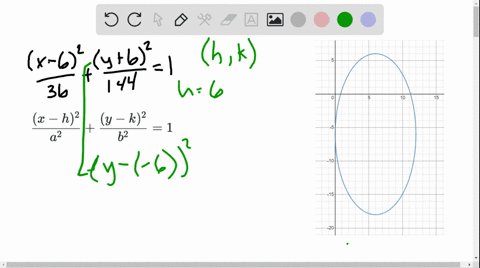
Find the equation of straight lines which pass through $(7,1)$,and divide the circumference of the circle $x^2y^2=100$ into two arcs whose lengths are in the ratio $31$View more examples » Access instant learning tools Get immediate feedback and guidance with stepbystep solutions and Wolfram Problem Generator Learn Explanation The equation of a circle is given by (x −h)2 (y −k)2 = r2 with center (h,k) and radius r We have the equation x2 y2 = 100, where the origin is our center since we have no h or k value We also know from √100 that we have radius 10 We can now graph this circle knowing we are centered at the origin, and we have a radius




Solved 1 Name And Sketch The Surfaces A 4 X2 Y2 16 2 Chegg Com




X 2 Xy Y 2 100
Integrate 1/(cos(x)2) from 0 to 2pi;Consider the hyperbola H x 2 − y 2 = 1 and a circle S with centre N (x 2 , 0) Suppose that H and S touch each other at a point P (x 1 , y 1 ) with x 1 > 1 and y 1 > 0 the common tangent to H and S at P intersects the Xaxis at point MConicsectionscalculator en Related Symbolab blog posts My Notebook, the Symbolab way Math notebooks have been around for hundreds of years You write down problems, solutions and



Solved Graph Each Equation Frac X 2 2 64 Frac Y 2 2 100 1




Graph The Solid Common To The Cylinders X 2 Z 2 100 And Y 2 Z 2 100 Using Maple And Find The Volume Of The Region Common To The Cylinders Study Com
If x 2 y 2 x 2 y 2 is equal to any other value between 0 and 9, 0 and 9, then g (x, y) g (x, y) equals some other constant between 0 and 3 0 and 3 The surface described by this function is a hemisphere centered at the origin with radius 3 3 as shown in the following graph z = 100 − 4 x 2 − 25 y 2 z = 100X^2 y^2 = 100 where the slope is 3/4 smaller y value (x,y) larger y value (x,y) Answer by josgarithmetic() (Show Source) You can put this solution on YOUR website!Answer to Let f(x,y) = \\sqrt{100 x^2 y^2} a Sketch the domain and the level sets in one graph b Find the gradient at the point (2,3)




Factoring 4 Warm Up Answers 2x 2 X 3 2 X 3 X 6 3 X 10 X 10 4 Y 2 3x 8 1 2x 3 6x 2 2 X 2 9x X 3xy Ppt Download



Calculus Find Dy Dt For X 2 Y 2 100 Youtube
If x = a(cosθ logtanθ/2), y = asinθ , find dy/dx at θ = π/4 asked in Continuity and Differentiability by KumkumBharti ( 539k points) continuity1Sketch the circle whose equation is x 2 2 y chord 2Draw the circles x 2 2 2 y 2 y = 100 Using the same system of coordinate axes, graph the line x 3= 10, which should intersect the circle twice at A = (10, 0) and at another point B in the second quadrantEstimate the coordinates of B Now use algebra to find them exactlyX 2 0 = 100 x 2 0 = 100 Add x 2 x 2 and 0 0 x 2 = 100 x 2 = 100 x 2 = 100 x 2 = 100 Take the square root of both sides of the equation to eliminate the exponent on the left side x = ± √ 100 x = ± 100 The complete solution is the result of both the



Solution Identify The Type Of Conic Sections That Has The Equation 4x 2 25y 2 100 And Identfy Its Domain And Range




X 2 Xy Y 2 100
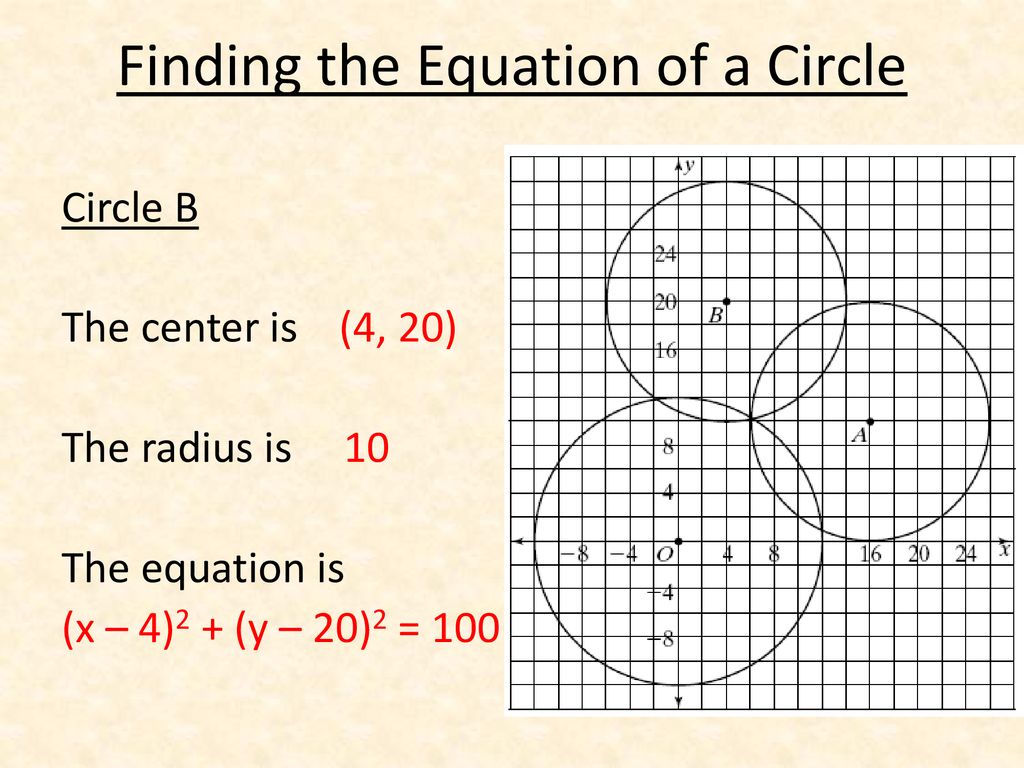
Question 3(Multiple Choice Worth 2 points) Write the equation 4x – 3y = 12 in the form y = mx b Oy = t 4 o y = 3x – 12 o IN Y ft 4 Oy = x 4 Previous, and you can find the corresponding y coordinate for eachI want to grab a circle based on its equation And the equation we have is X squared, plus y squared equals 100 I'm gonna take that simplified version of the standard equation, and I'm gonna ride it back in its expanded former because X comes from X minus zero and we're gonna square that quantity Why squared actually comes from why minus zero squared, writing it like the standard



Find An Equation Of The Tangent Line To The Graph At Chegg Com



Drill Find The Area And Circumference Of Each Circle In Terms Of Pi With The Given Information For Each Circle Radius 5 In Diameter 14 Ft Radius Ppt Download
{(x, y) / x 2 y 2 = 100, where x, y ∈ W} We have, x 2 y 2 = 100 When x = 0 and y = 10, x 2 y 2 = 0 2 10 2 = 100 When x = 6 and y = 8, x 2 y 2 = 6 2 8Simple and best practice solution for (x9)2(y6)2=100 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



Madrasmaths Com




The Area Of The Blue Circle Centered At The Origin Which Is Inscribed In The Parabola Y X 2 100 Can Be Expressed As Frac A B Pi Mathematics Stack Exchange
Online math solver with free step by step solutions to algebra, calculus, and other math problems Get help on the web or with our math appIf one of the variables x, y or z is missing from the equation of a surface, then the surface is a cylinder Note When you are dealing with surfaces, it is important to recognize that an equation like x2 y2 = 1 represents a cylinder and not a circle The trace of the cylinder x 2 y = 1 in the xyplane is the circle with equations x2 y2X, y ≥ 0 Minimize & Maximize Z = x 2y Subject to, x 2y ≥ 100 2x y ≤ 0 2x y ≤ 0 x, y, ≥ 0 ∴ Z = 400 is maximum at (0, 0) Also, Z is minimum at two points (0, 50) & (, 40) ∴ Z = 100 is minimum at all points joining (0, 50) & (, 40)



Solved How Do I Find The Dimensions Of The Rectangle With Maximum Perimeter That Can Be Inscribed In X 2 Y 2 100 Course Hero



How Do You Determine The Domain And Range Of The Relation X 2 Y 2 1 And X 2 Y 2 100 I Know It Makes A Circle But I M Just Confused About The Enotes Com
Example 4 Factor 49 x 2 − 100 y 2 Solution Here we have a binomial with two variables and recognize that it is a difference of squares Therefore, a = 7 x and b = 10 y Substitute into the formula for difference of squaresUse a parametrization to find the flux {eq}\iint_SFnd\sigma {/eq} of the field F = 5z k across the portion of the sphere {eq}x^2 y^2 z^2 = 100 {/eq} in the first octant in the direction away{(x, y) / x 2 y 2 = 100 where x, y ∈ W} We have, x 2 y 2 = 100 When x = 0 and y = 10, x 2 y 2 = 0 2 10 2 = 100 When x = 6 and y = 8, x 2 y 2 = 6 2 8 2




Express X Y X 2 Y 2 100 Where X Y Belongs To W As A Set Of Ordered Pairs Asap Maths Relations And Functions Meritnation Com




X 2 Y 2 Z 2 100 Xy Yz Zx 2 Brainly In
Sin (x)cos (y)=05 2x−3y=1 cos (x^2)=y (x−3) (x3)=y^2 y=x^2 If you don't include an equals sign, it will assume you mean " =0 " It has not been well tested, so have fun with it, but don't trust it If it gives you problems, let me know Note it may take a few seconds to finish, because it has to do lots of calculationsGet an answer for 'Solve the system of equations algebraically x^2y^2=100 xy=2' and find homework help for other algebra1 questions at eNotesAnd now solve the difference of two squares with a = 36 and b = 4y 2 Solution Factor the equation (rearranged) 36 − 4 y 2 using the identity a 2 − b 2 = ( a b) ( a − b) First factor out the GCF 4 ( 9 − y 2) Both terms are perfect squares so from a 2 b 2 we can find a and b
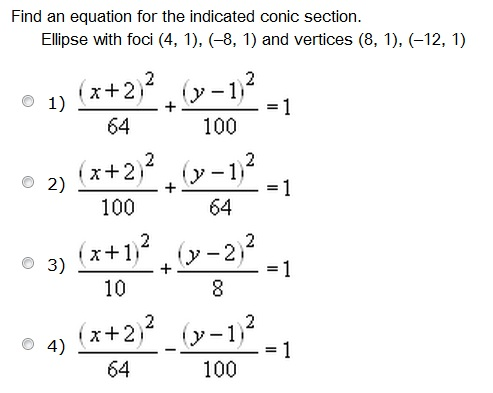



Solved Find An Equation For The Indicated Conic Section Chegg Com




Solved Question 3 Find An Equation For The Sphere That Is Chegg Com
Transcript Ex 53, 5 Find 𝑑𝑦/𝑑𝑥 in, 𝑥2 𝑥𝑦 𝑦2 = 100 𝑥2 𝑥𝑦 𝑦2 = 100 Differentiating both sides 𝑤𝑟𝑡𝑥Divide y, the coefficient of the x term, by 2 to get \frac{y}{2} Then add the square of \frac{y}{2} to both sides of the equation This step makes the left hand side of the equation a perfect square The parabola y^2 = 4x 1 divides the disc x^2 y^2 ≤ 1 into two regions with areas A1 and Then A1 – equals asked in Mathematics by RenuK ( 6k points)




Solved The Hemisphere X 2 Y 2 Z 2 100 For Z 0 A Chegg Com



Does The Equation X2 Y2 100 Define Y As A Function Gauthmath
Click here👆to get an answer to your question ️ Find dydx , if x^2 xy y^2 = 10048 Part 2 Consumption and Production From the fi rst two conditions, λ = 025 x – 05 Y 05 = 05 X 05 Y – 05 Y = 2X Substituting into the third FOC, weExample 2 if x = 10 and y is 4 (10 4) 2 = 10 2 2·10·4 4 2 = 100 80 16 = 36 The opposite is also true 25 a 4a 2 = 5 2 2·2·5 (2a) 2 = (5 2a) 2 Consequences of the above formulas




Recognise And Use X2 Y2 R2 Ppt Download




Example 1 Graph An Equation Of A Hyperbola Graph 25y 2 4x 2 100 Identify The Vertices Foci And Asymptotes Of The Hyperbola Solution Step 1 Rewrite Ppt Download
The equation x2y2−16x6y73=100 can be rewritten as g(x)2(y3)2=100Write an expression for g(x) Get the answers you need, now!Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




Q5 If X 2 Xy Y 2 100 Find Dy Dx Implicit Function If X2 Xy Y2 100 Find Dy Dx Youtube



1



Solution Show That The Tangents To The Circle X 2 Y 2 100 At The Points 6 8 And 8 6 Are Perpendicular To Each Other




Answered Graph The Ellipse X2 64 Y2 100 1 Bartleby



Solved Consider The Point 6 8 On The Circle X 2 Y 2 100 A Determine The Primary Trigonometric Ratios For The Principal Angle B Determine Course Hero



Which Identity Do We Use To Factorise X 2 Frac Y 2 100 Frac Xy 5 A A B 2 A 2 B 2 2ab B A B 2 A 2 B 2 2ab C A B C 2 A 2 B 2 C 2 2ab 2bc 2ca D A B C 2 A 2 B 2 C 2 2ab 2bc 2ca Snapsolve




Se11g01 02 Gif




Factorize X 2 Y 2 100 Maths Questions



Solution Sketch The Circle Whose Equation Is X2 Y2 100 Using The Same System Of Coordinate Axes Graph The Line X 3y 10 Which Should Intersect The Circle Twice At A 10 0



X 2y 4z 2




Solved Compute The Volume Of The Solid Bounded Above By The Chegg Com




Find Dy Dx In The Following X 2 X Y Y 2 100




X 2 Y 2 100 Ferarwan



Solution How Can I Solve The System Of Equations X 2 Y 2 100 3x Y 10
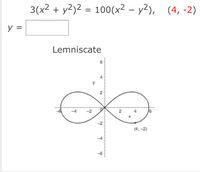



Answered 3 X2 Y2 2 100 X Y2 4 2 Y Bartleby
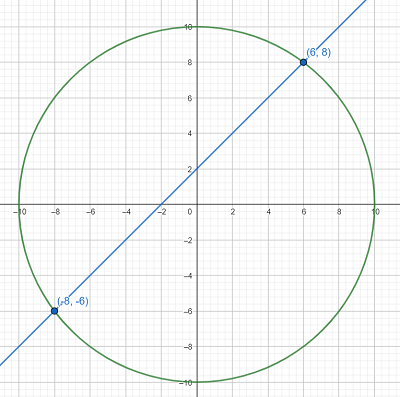



Solve The System Graphically X 2 Y 2 100 Y X 2 Study Com




Ok Because This Confuses Me Why Can T I Just Do 30 Is This An Error By The Book Or What This Is The Ultimate Guide To Act Math Btw R Act



Npsk12 Com



Ellipses And Hyperbolae



Solution Find All Points On The Circle X 2 Y 2 100 Where The Slope Is 3 4




X 2 Y 2 100 Find Dy Dx Using Implicit Differentiation Youtube



Equation Of A Circle




Solved If X 2 Y 2 100 Find Dy Dx Find An Equation Of Chegg Com




Find Dx Dy For X2 Xy Y2 100 Mathematics Shaalaa Com



The Equation Of A Circle Is X 2 Y 2 100 Write The Equ Quizlet




Solved What Curve Is Represented By The Given Parametric Equations Xft 10 Sin 10t Y T 10 Cos Lot 0 T 2t 0ax Y 2 101 0b Y 99 0c X Y 2 100 01 2 Y 300 Oex Y 0




Let F X Y Sqrt 100 X 2 Y 2 A Sketch The Domain And The Level Sets In One Graph B Find The Gradient At The Point 2 3 C Find The Limit



Circles Objectives Assignment Ppt Download




Ppt Higher Unit 2 Powerpoint Presentation Free Download Id



Solved Graph Each Equation X 2 Y 2 100
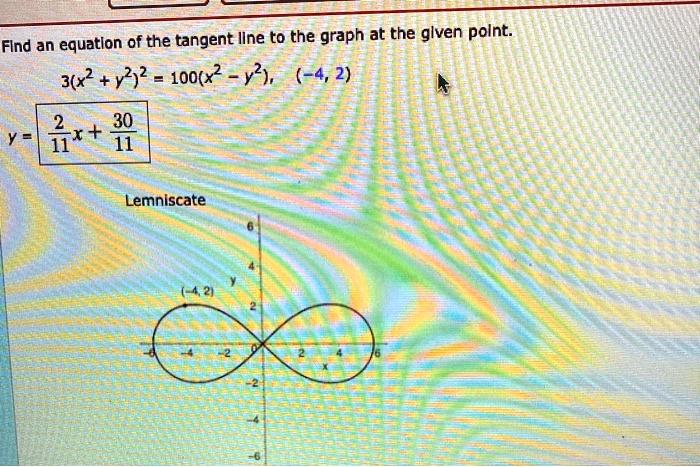



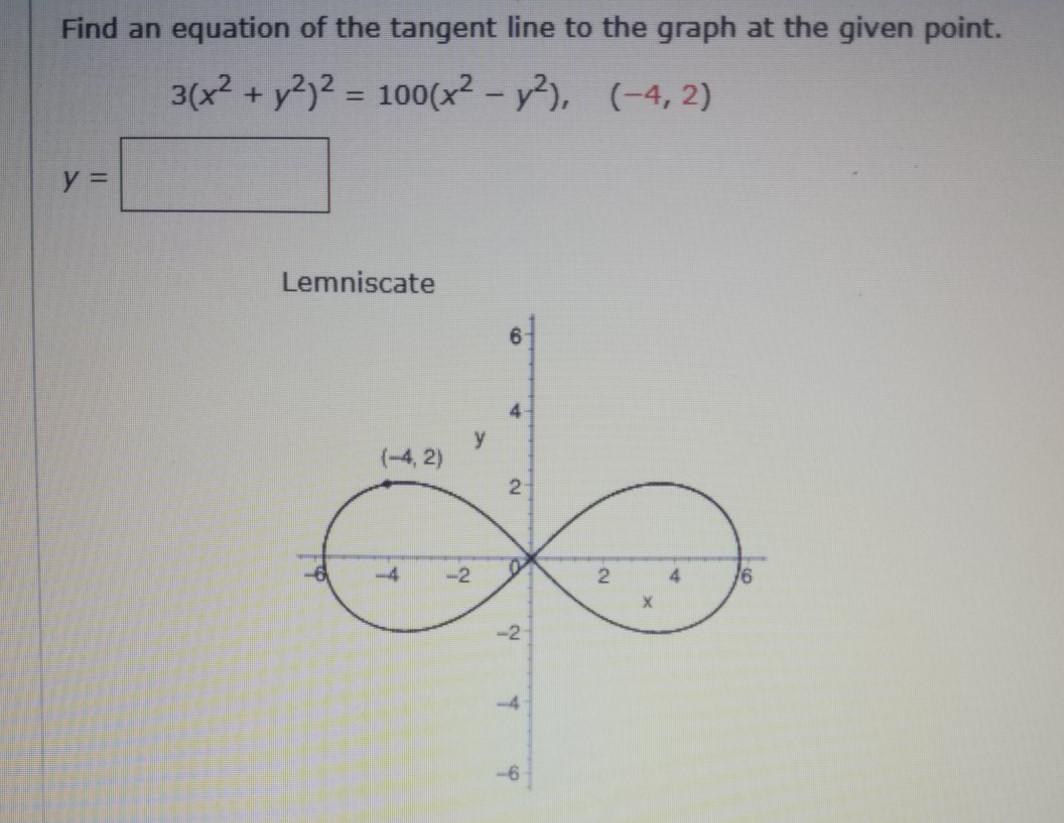
Solved Equation Of The Tangent Ilne To The Graph At The Glven Polnt Flnd An 3 X2 72 2 100 X2 Y 4 2 X 30 11 11 Lemnlscate



What Is The Eccentricity Of The Curve 4 X2 Y2 100 Mathematics Topperlearning Com 6du56yqxx
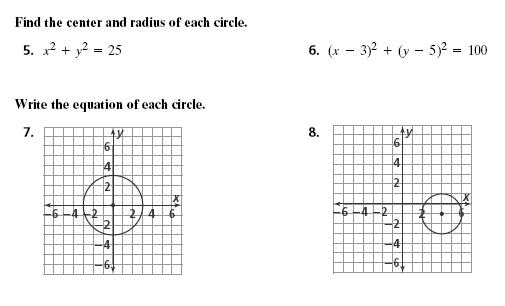



Solved Find The Center And Radius Of Each Circle X2 Y2 Chegg Com



Mathematics Help Pleaseee The Student Room




Ex 11 3 4 X2 25 Y2 100 1 Find Foci Latus Rectum Ex 11 3



If The Line Y Mx C Is A Common Tangent To The Hyperbola X 2 100 Y 2 64 1 And The Circle X 2 Y 2 36 Sarthaks Econnect Largest Online Education Community




The Equation Of The Outer Circles Are X 12 2 Y 15 2 25 And Plainmath




Factorize X 2 Y 2 100 Brainly In
%5E2-100.png)



Graph Of Y 4 X 5 2 100



Mathematics Help Pleaseee The Student Room



For X 2 100 Y 2 25 1 Prove That A E 5 2 B Sa S A 25 Where S S Are Foci A Is Vertex Sarthaks Econnect Largest Online Education Community
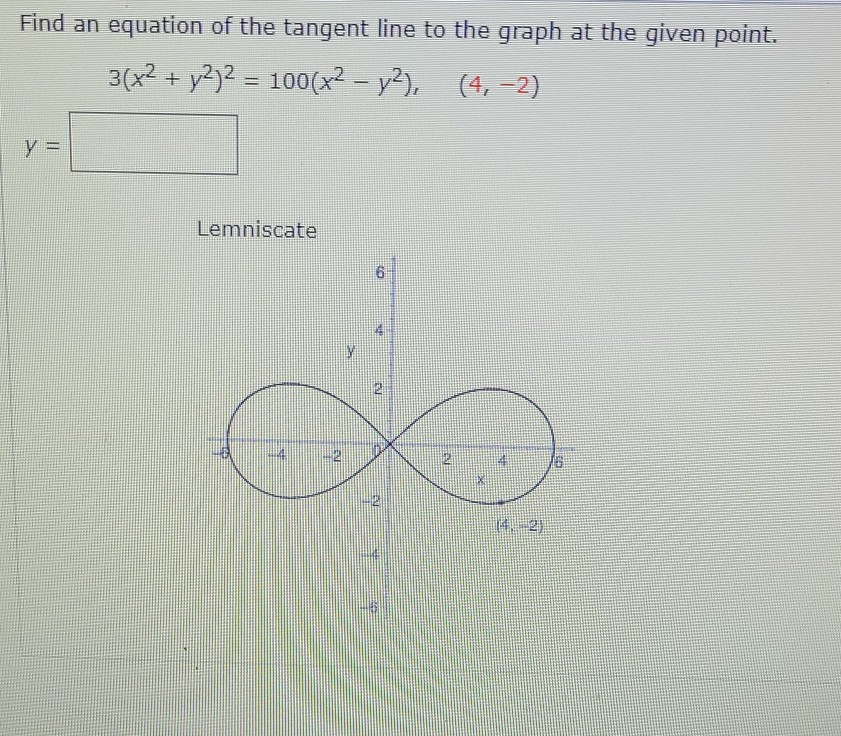



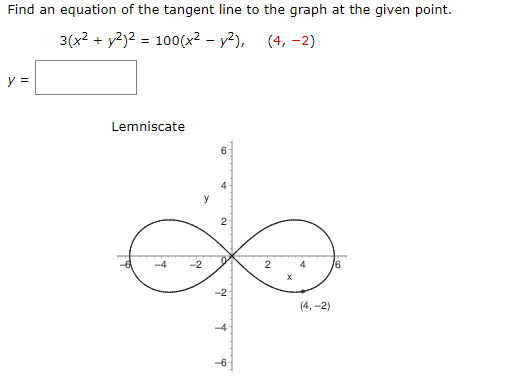
Solved Find An Equation Of The Tangent Line To The Graph At Chegg Com
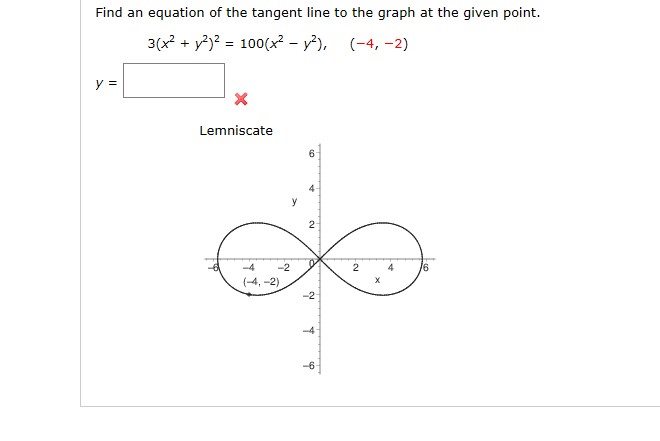



Find An Equation Of The Tangent Line To The Graph At The Given Point Socratic
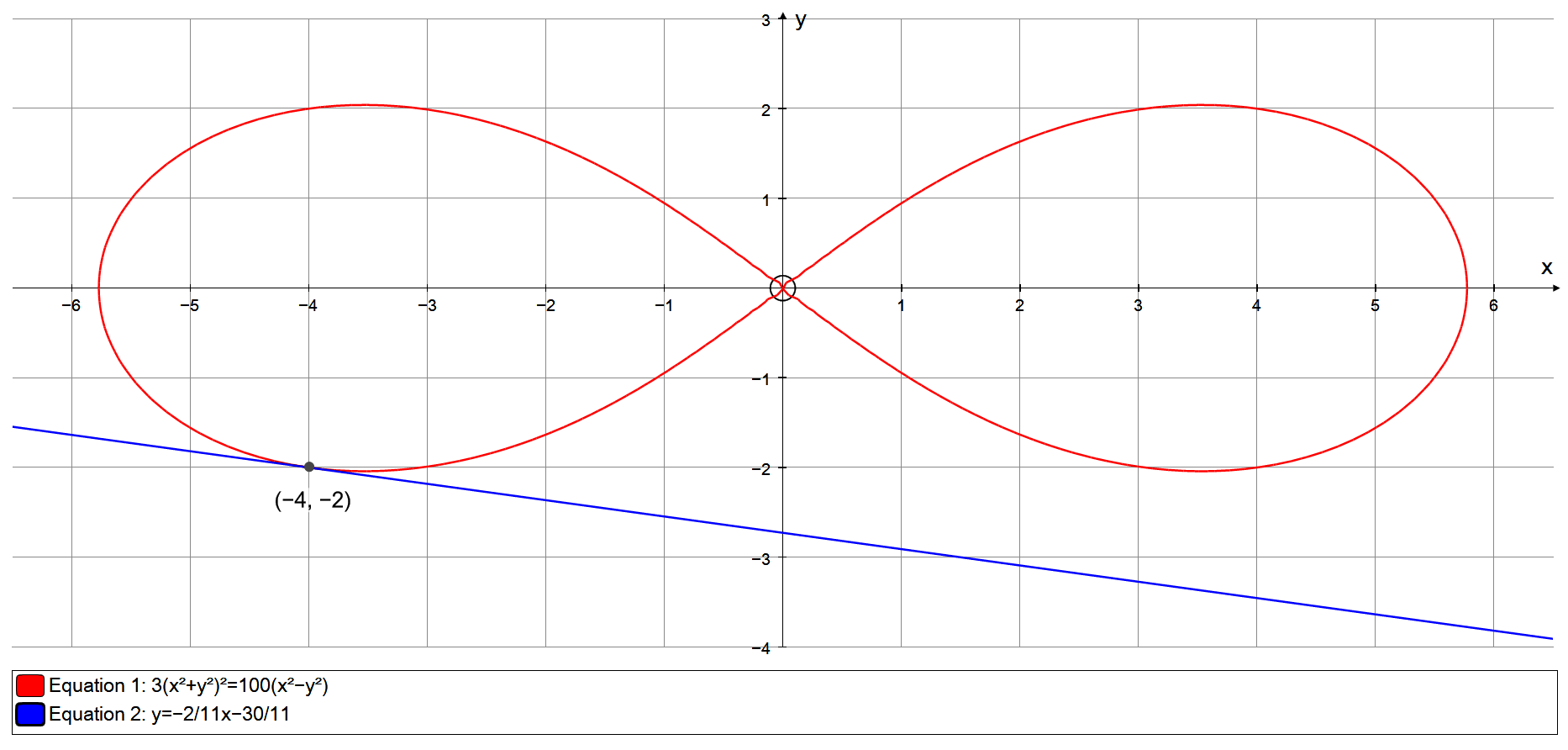



Find An Equation Of The Tangent Line To The Graph At The Given Point Socratic




Equation Of Tangent Line To Circle X 2 Y 2 100 At Point 6 8 Youtube
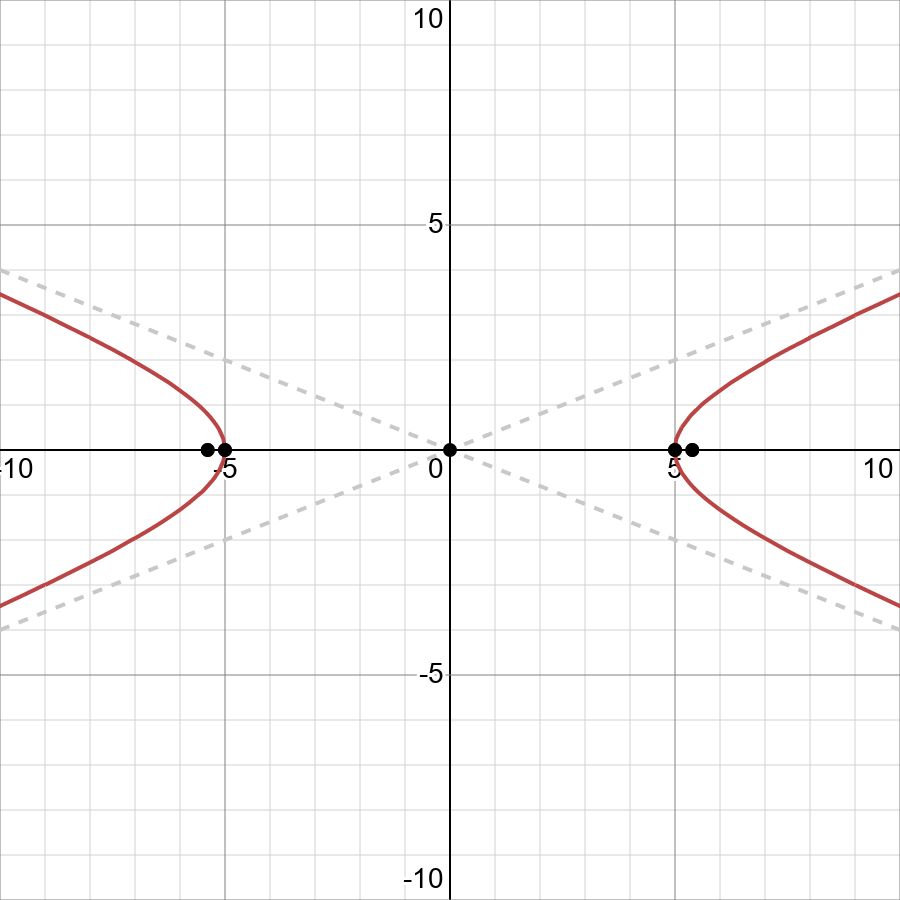



Graph 4x 2 25y 2 100 Displaystyle 4 X 2 25 Y 2 100 Snapsolve




Ex 5 3 5 Find Dy Dx In X2 Xy Y2 100 Class 12
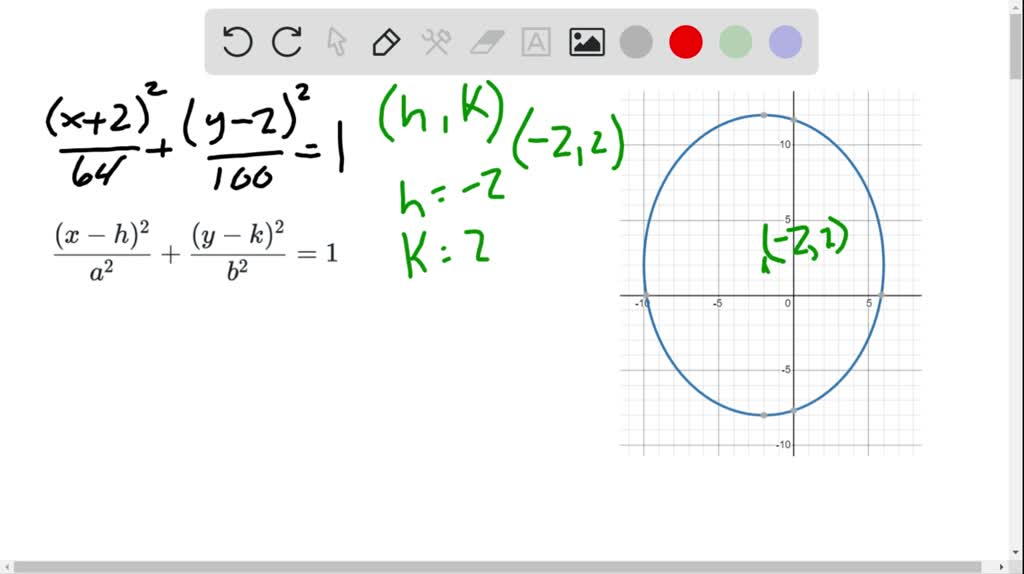



Solved Graph Each Equation Frac X 2 2 64 Frac Y 2 2 100 1




Solved Find Dy Dx By Implicit Differentiation X 2 Y 2 Chegg Com
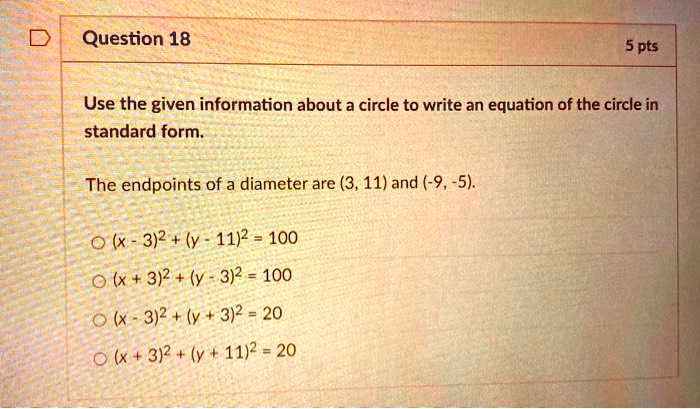



Solved Question 18 5 Pts Use The Given Information About A Circle To Write An Equation Of The Circle In Standard Form The Endpoints Of A Diameter Are 3 11 And 9 5 3 2



Iii Sketch The Graph Of The Following Equation 1 Gauthmath
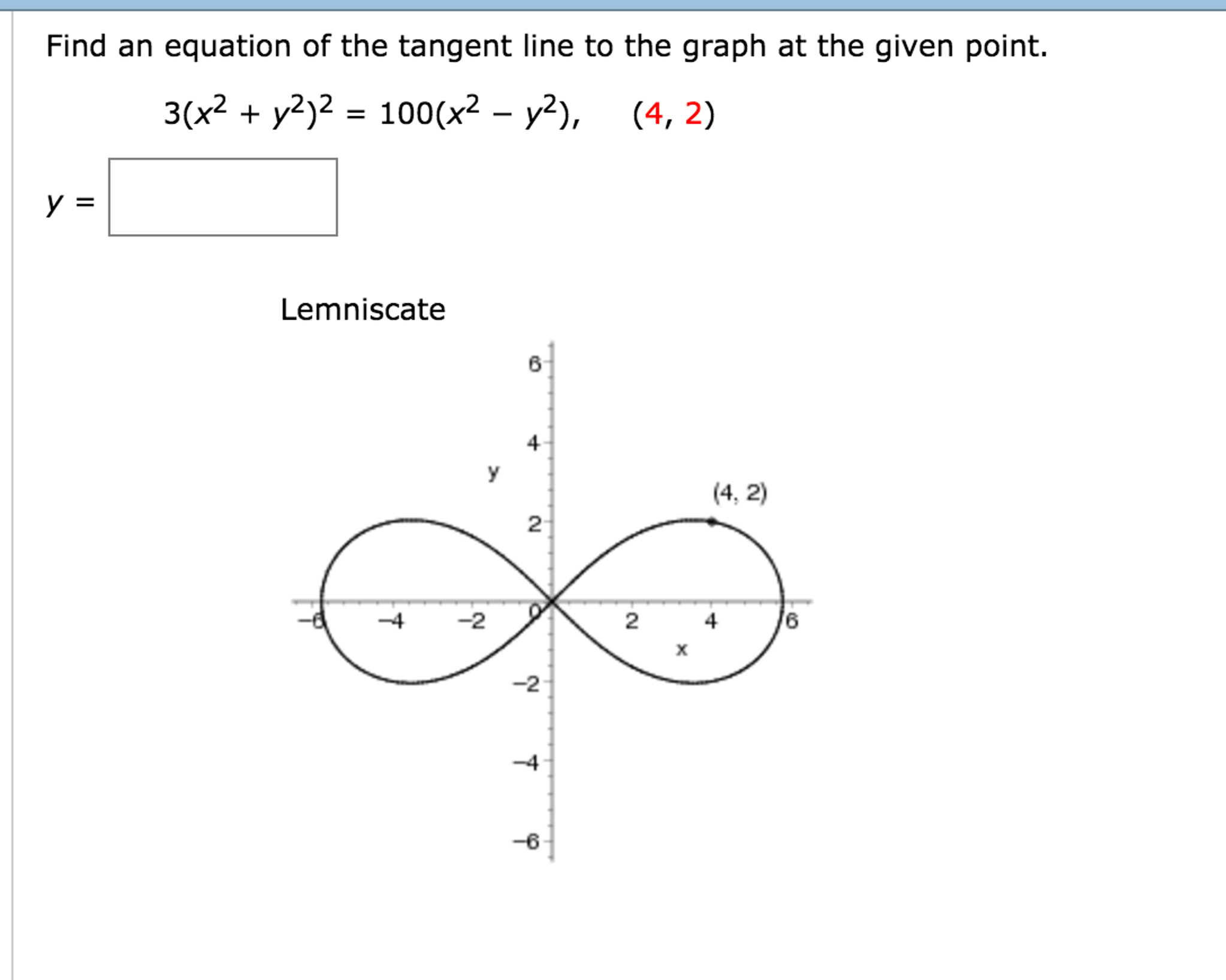



Solved Find An Equation Of The Tangent Line To The Graph At Chegg Com




Ex 11 3 4 X2 25 Y2 100 1 Find Foci Latus Rectum Ex 11 3
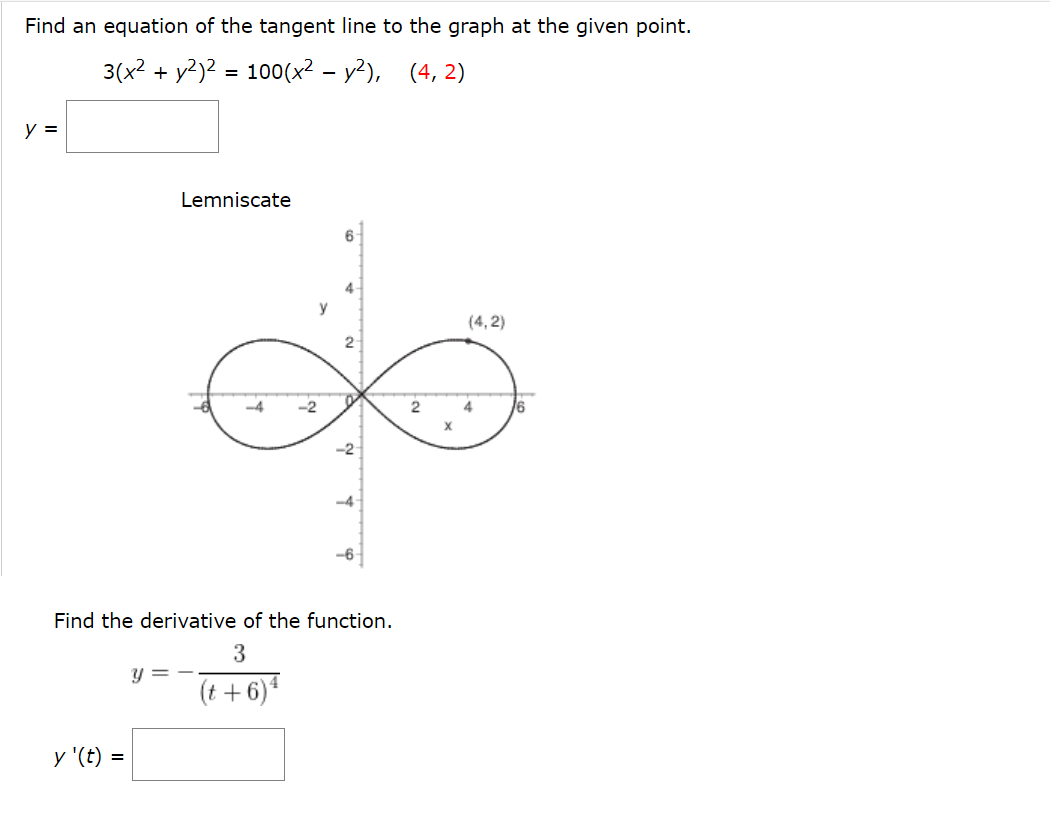



Solved Find An Equation Of The Tangent Line To The Graph At Chegg Com




Chord Ab Of The Circle X 2 Y 2 100 Passes Through The Point 7 1 And Subtends An Angle Youtube




0 7 Let A 71 2 1 2 1 1 1 2 2 B 1 Homeworklib




Trevor Is Analyzing A Circle Y 2 X 2 100 And A Linear Function G X Will They Brainly Com




What Is The Center Of The Circle X2 Y2 100 Brainly Com



If X 2 Y 2 100 And X Y 4 3 Then What Is The Value Of X 2 Y 2 Youtube



1 Given The Spheres X 7 2 Y 3 2 22 49 And X Itprospt




A Particle Moves On The Circle X 2 Y 2 100 In The Xy Plane For Time T 0 At The Time When The Particle Is At The Point 8 6 The Value Of Dx Dt Is 5 What Is




Circle Has The Equation X 2 Y 2 2x 2y 14 0 How Do You Graph The Circle Using The Center H K Radius R Homeworklib



Solution The Linear Equation X2 Y2 100 If X 6 Value S Of Y Select One 1 None Of The Above 2 8 3 8 4 8 Or 8



1



If X Y 2 100 And Xy What S The Value Of X 2 Y 2 Brainly Com




Write The Equation Of 2 Circle Where A 1 2 And B 7 Itprospt
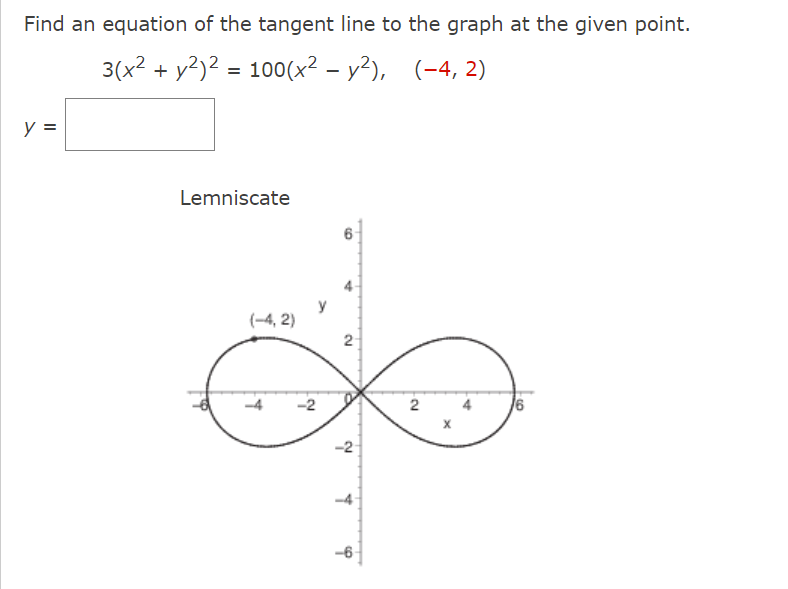



Solved Find An Equation Of The Tangent Line To The Graph At Chegg Com
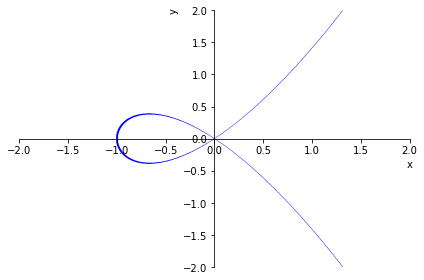



Implicit Curve Plots May Better Use Matplotlib Contour Issue 056 Sympy Sympy Github




Ex 2 5 3 Iii Factorise X 2 Y 2 100 Using Appropriate Identities




Solved Find The Equation Of The Tangent Line In Point Slope Form To The Graph At The Given Point 1 Y V2x2 7 4 5 2 Y 4x3 3 2 1 1 3 Y




Solved B Solving The Equation X2 Y2 100 We Get Y Y Chegg Com




What Is The Equation Of The Circle With Center 0 1 And A Radius



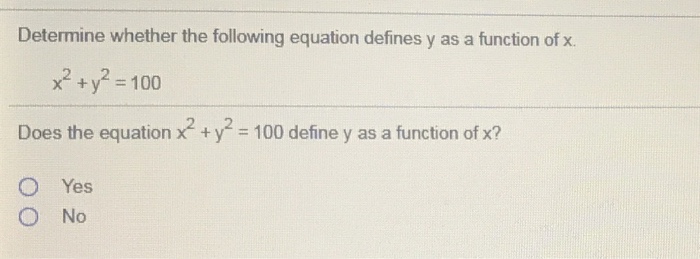
Solution Determine Whether The Following Equation Defines Y As A Function Of X X 2 Y 100 Does The Equation X 2 Y 100 Define Y As A Function Of X
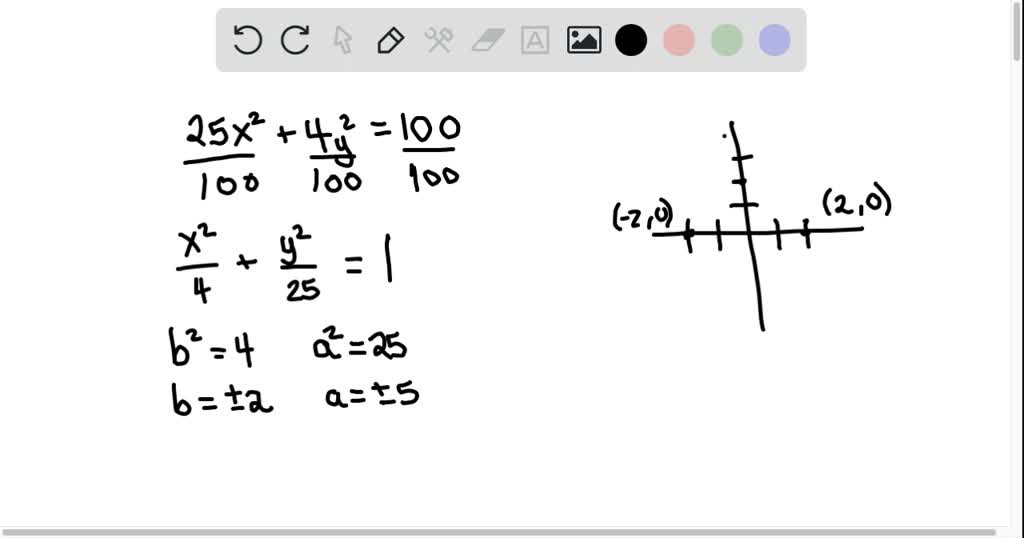



Solved Determine The Foci The Eccentricity And The Directrices For Each Ellipse And Hyperbola A 4 X 2 25 Y 2 100 B 4 X 2 25 Y 2 100



Image Graph Of Equation X 2 Y 2 100 Equation
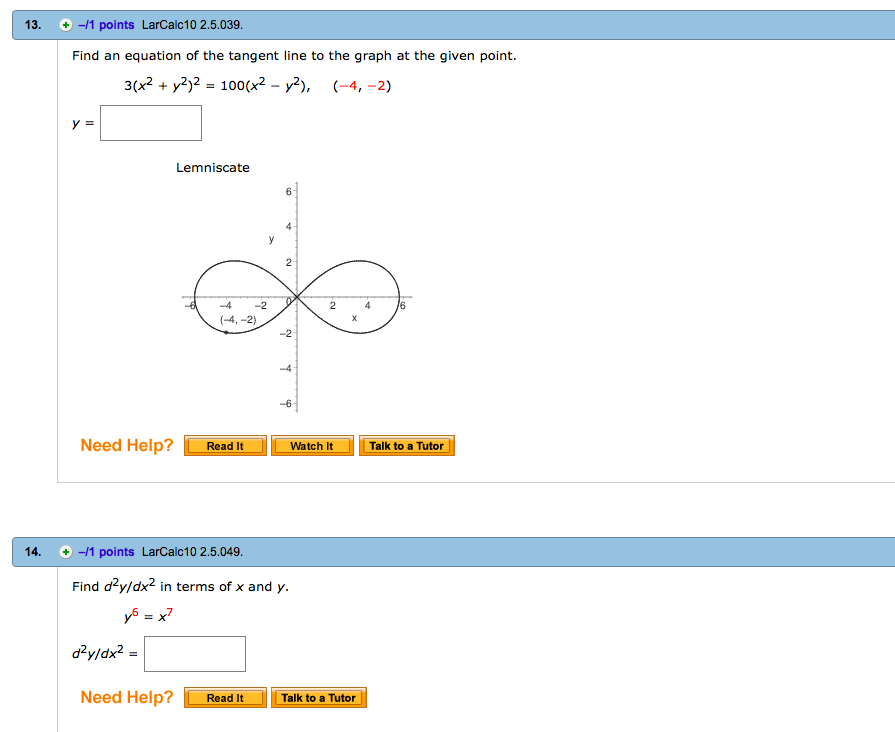



Solved 13 Il Points Larcalc10 2 5 039 Find An Equation Of Chegg Com



0 件のコメント:
コメントを投稿